5.Longest Palindromic Substring

This question on LeetCode is similar to the 516. Longest Palindromic Subsequence. Therefore, I'm also using the same dynamic programming solution to solve. However, there are slight differences. Here, we are using the dp array to store the boolean value indicating whether the substring from index i to j is a palindromic substring.

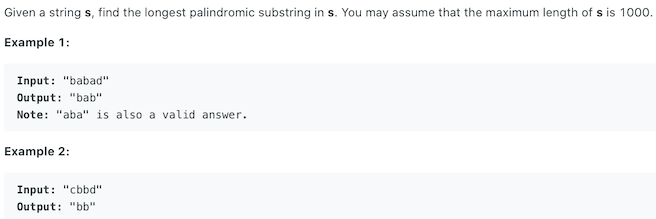
Question

Solution

We create a 2D-array dp, where dp[i][j] contains the boolean answer that the current substring formed from index i to j in s is palindromic or not.
There are three conditions following:

i == j
It is always true that single-word substrings are palindromes
s[i] == s[j]
If the substring between indices i+1 and j-1 is a palindrome, then we can conclude that the current substring is also a palindrome. However, we must be cautious when two-word substrings like substring dd in the string (bab'dd') is palindromes as well cause the default value of boolean array is false. So, the dp[4][3] will get false in this situation. That reason why I added j - i == 1 to the conditional expression.
s[i] != s[j]
If s[i] is not equal to s[j], then this substring cannot be a palindrome.

//Time complexity: O(n^2)
//Space complexity: O(n^2)
class Solution {
    public String longestPalindrome(String s) {
        if(s.length() < 2) {
            return s;
        }

        String maxSubString = "";
        boolean[][] dp = new boolean[s.length()][s.length()];
        for(int i=s.length()-1;i>=0;i--) {
            for(int j=i;j<s.length();j++) {
                if(i == j) {
                    dp[i][j] = true;
                } else if(s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i+1][j-1] || j - i == 1;
                } else {
                    dp[i][j] = false;
                }
                if(dp[i][j] && j-i+1 > maxSubString.length()) {
                    maxSubString = s.substring(i, j+1);
                }
            }
        }
        return maxSubString;
    }
}

Kevin Blog

5.Longest Palindromic Substring

Question

Solution

Similar Questions